Algorithms for unweighted sampling without replacement

I am currently working on weighted sampling for dqrng, c.f. #72, for which also have to decide on the algorithm(s) to use for weighted sampling without replacement. Before looking at that I wanted to verify my decisions for the unweighted case.

Using the new header file dqrng_sample.h from the currently released version v0.3.1 and the ability to access the global RNG from the current development version, it is easy to write functions that make use of the three provided algorithms: Partial Fisher-Yates shuffle, rejection sampling using a hash set and rejection sampling using a bit set:

#include <Rcpp.h>
// [[Rcpp::depends(dqrng)]]
// requires dqrng > v0.3.1
#include <dqrng.h>
#include <dqrng_sample.h>

// [[Rcpp::export]]
Rcpp::IntegerVector sample_shuffle(int n, int size) {
  dqrng::random_64bit_accessor rng;
  return dqrng::sample::no_replacement_shuffle<Rcpp::IntegerVector, uint32_t>
    (rng, uint32_t(n), uint32_t(size), 1);
}

// [[Rcpp::export]]
Rcpp::IntegerVector sample_hashset(int n, int size) {
  dqrng::random_64bit_accessor rng;
  using set_t = dqrng::minimal_hash_set<uint32_t>;
      
  return dqrng::sample::no_replacement_set<Rcpp::IntegerVector, uint32_t, set_t>
    (rng, uint32_t(n), uint32_t(size), 1);
}

// [[Rcpp::export]]
Rcpp::IntegerVector sample_bitset(int n, int size) {
  dqrng::random_64bit_accessor rng;
  using set_t = dqrng::minimal_bit_set;
      
  return dqrng::sample::no_replacement_set<Rcpp::IntegerVector, uint32_t, set_t>
    (rng, uint32_t(n), uint32_t(size), 1);
}

Next we can benchmark these algorithms against each other and the implementation from R itself for different population sizes n and selection ratios r:

bp <- bench::press(
  n = 10^(1:8),
  r = c(0.7, 0.5, 10^-(1:4)),
  {
    size <- ceiling(r * n)
    bench::mark(
      sample.int(n, size),
      sample_shuffle(n, size),
      sample_hashset(n, size),
      sample_bitset(n, size),
      check = FALSE,
      time_unit = "s"
    )
  }
) |> mutate(label = as.factor(attr(expression, "description")))

Warning: Some expressions had a GC in every iteration; so filtering is
disabled.

Warning: Some expressions had a GC in every iteration; so filtering is
disabled.

Warning: Some expressions had a GC in every iteration; so filtering is
disabled.

Warning: Some expressions had a GC in every iteration; so filtering is
disabled.

ggplot(bp, aes(x = n, y = median, color = label)) + 
  geom_line() + scale_x_log10() + scale_y_log10() + facet_wrap(vars(r))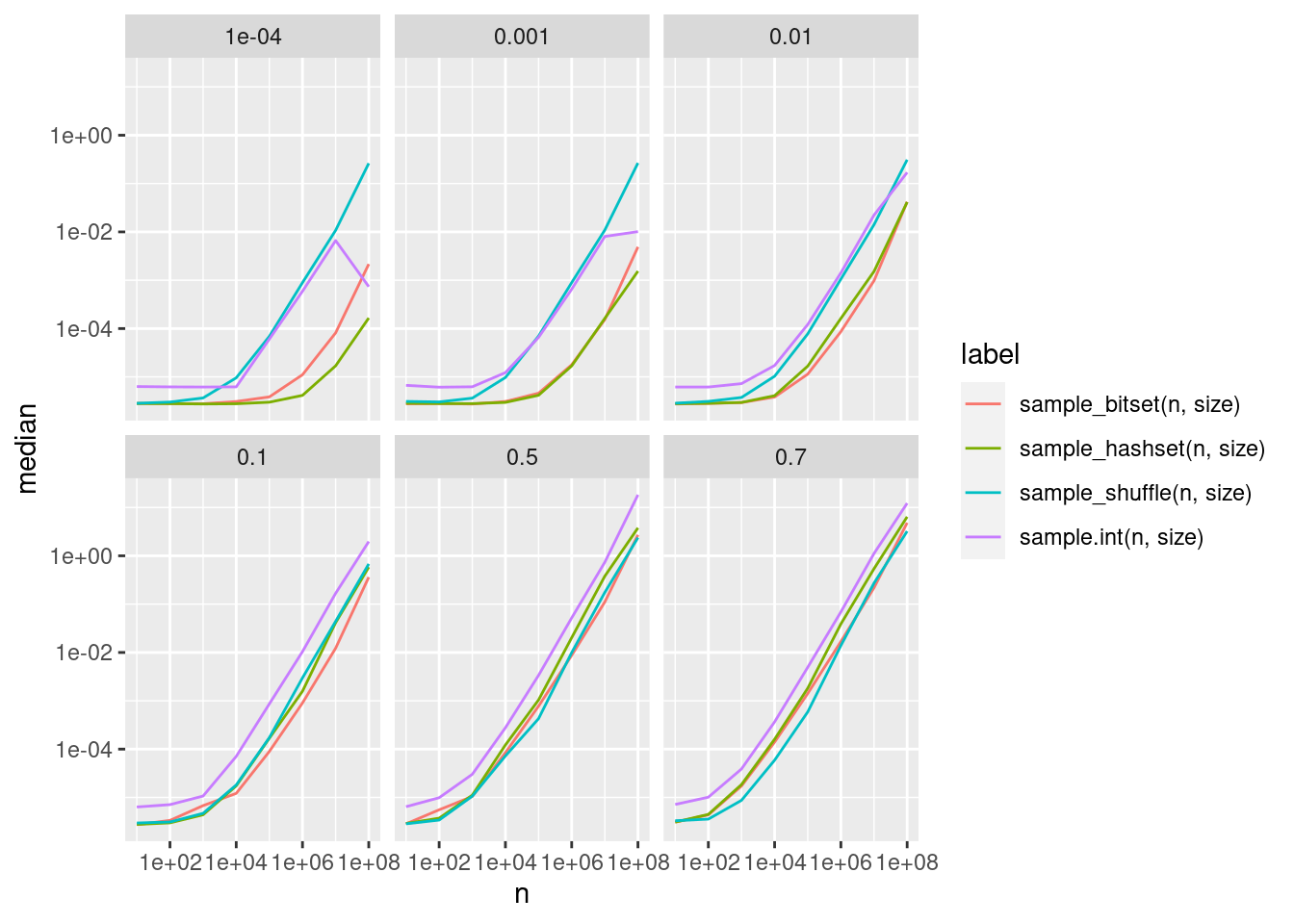

We learn:

The fastest method from dqrng is always faster than R itself.
The increased performance for R at n = 1e8 with low selection ratio is triggered by switching to a hash table. R should do this much earlier.
For the three methods from dqrng we see:
- For 0.5 < r the partial Fisher-Yates shuffle is optimal
- For 0.001 < r < 0.5 it is best to use rejection sampling using a bit set
- For 0.001 > r one should switch to rejection sampling using a hash set

This is exactly how it is implemented in dqrng::sample<VEC, INT>, which is quite reassuring.