// [[Rcpp::depends(dqrng,BH,sitmo)]]
#include <Rcpp.h>
#include <dqrng_distribution.h>
auto rng = dqrng::generator<>(42);
// [[Rcpp::export]]
Rcpp::IntegerVector sample_prob(int n, Rcpp::NumericVector prob) {
Rcpp::IntegerVector result(Rcpp::no_init(n));
double max_prob = Rcpp::max(prob);
uint32_t m(prob.length());
std::generate(result.begin(), result.end(),
[m, prob, max_prob] () {
while (true) {
int index = (*rng)(m);
if (dqrng::uniform01((*rng)()) < prob[index] / max_prob)
return index + 1;
}
});
return result;
} There is a long standing issue with my {dqrng} package: weighted sampling. Since implementing fast un-weighted sampling methods quite some time ago, I have now started looking into possibilities for weighted sampling.
The issue contains a reference to a blog post that is by now only available via the wayback machine. This blog post shows a stochastic acceptance method suggested by Lipowski and Lipowska (2012) (also at https://arxiv.org/abs/1109.3627), which appears very promising. Let’s try some simple tests before incorporating it into the package properly. The stochastic acceptance algorithm is very simple:
- Select randomly one of the individuals (say, \(i\)). The selection is done with uniform probability \(1/N\), which does not depend on the individual’s fitness \(w_i\).
- With probability \(w_i/w_\max\), where \(w_\max = \max\{w_i\}_{i=1}^N\) is the maximal fitness in the population, the selection is accepted. Otherwise, the procedure is repeated from step 1 (i.e., in the case of rejection, another selection attempt is made).
This can be implemented as:
First, let’s check that sampling still works as expected:
M <- 1e4
N <- 10
prob <- runif(N)
hist(sample.int(N, M, replace = TRUE, prob = prob), breaks = N)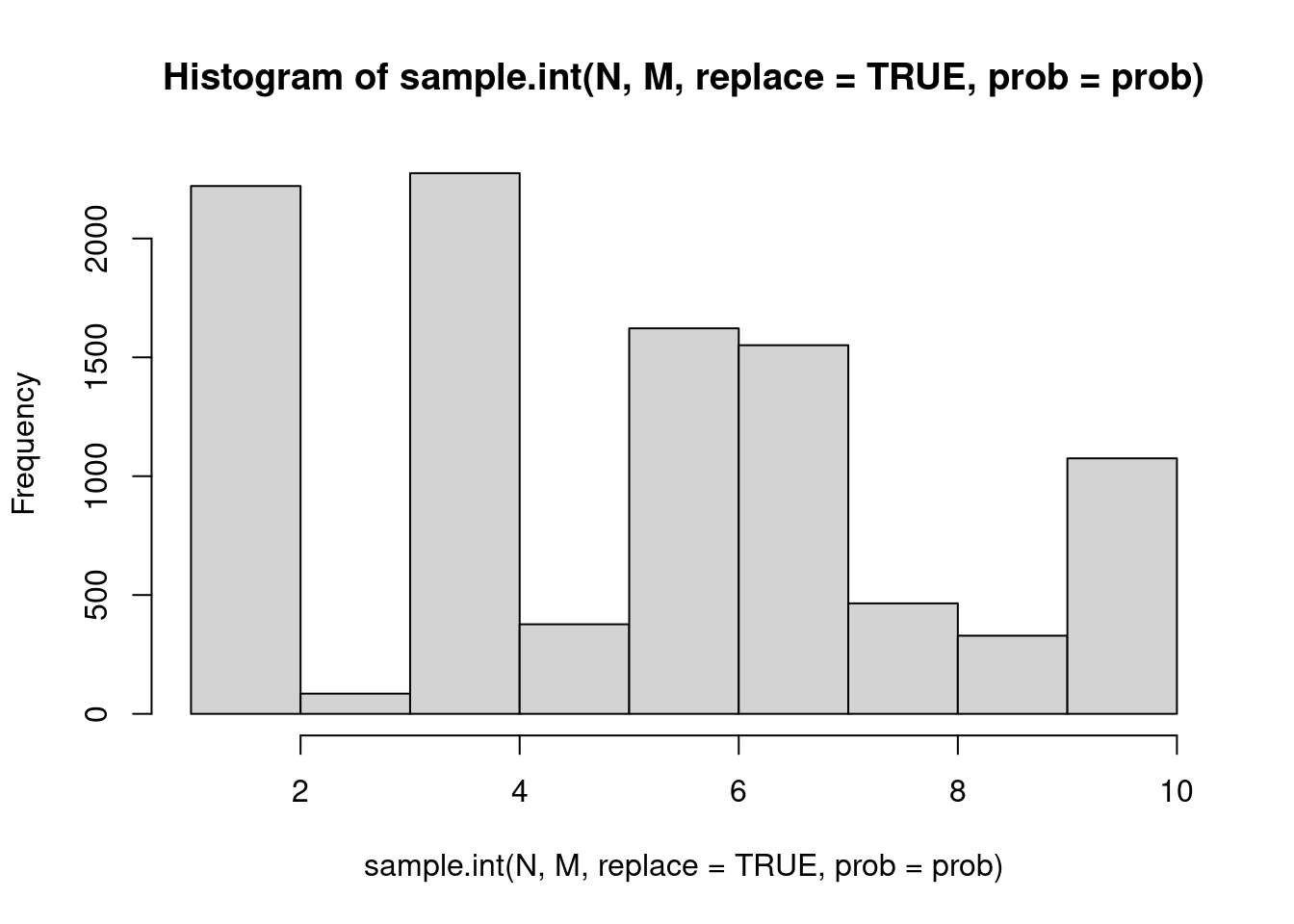
hist(sample_prob(M, prob = prob), breaks = N)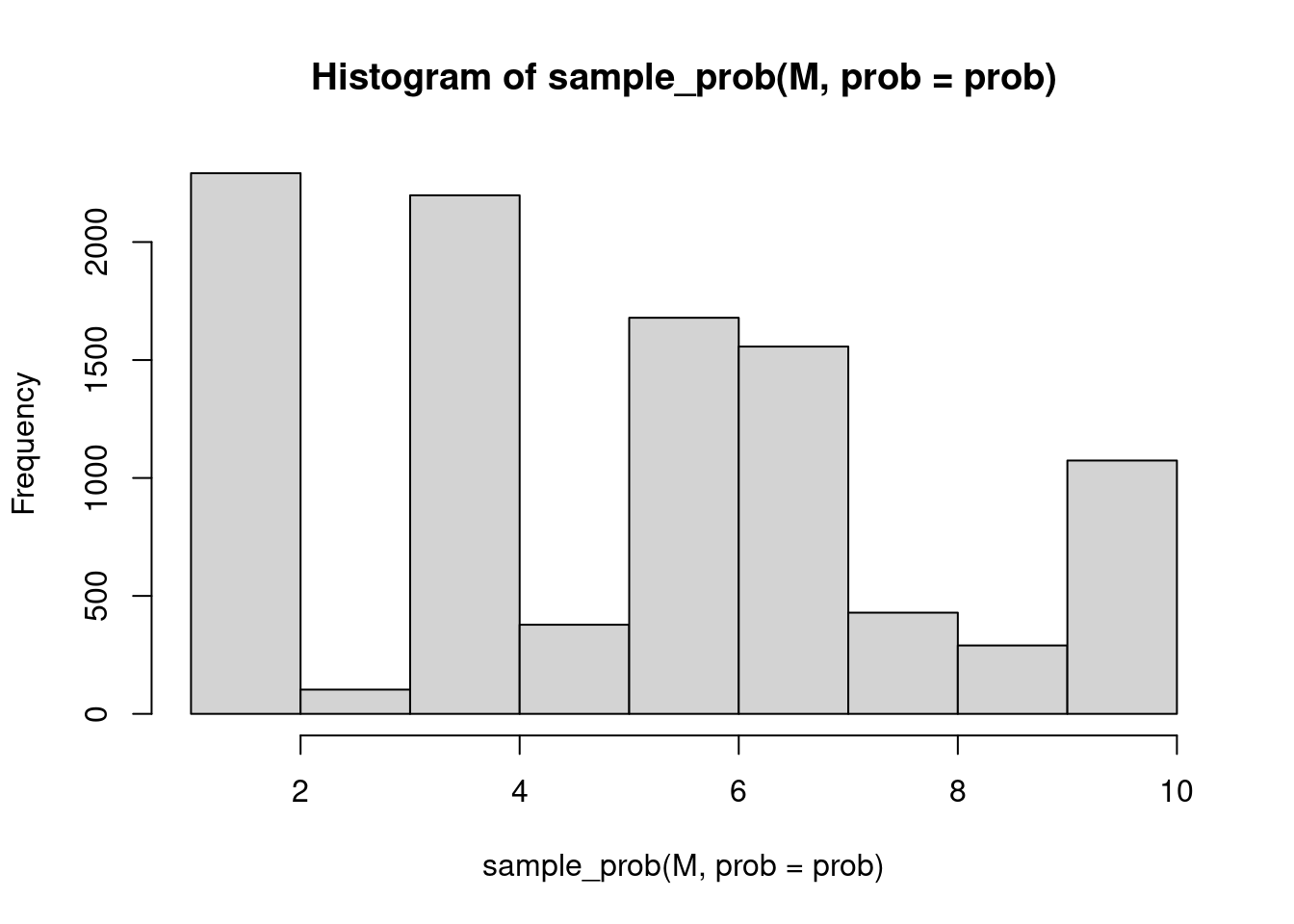
Eyeballing these histograms shows that they are very similar, i.e. the stochastic acceptance algorithm selects the ten possibilities with the same probabilities as R’s build in method.
Second, let’s look at performance:
bm <- bench::mark(
sample.int = sample.int(N, M, replace = TRUE, prob = prob),
sample_prob = sample_prob(M, prob = prob),
check = FALSE
)
knitr::kable(bm[, 1:6])| expression | min | median | itr/sec | mem_alloc | gc/sec |
|---|---|---|---|---|---|
| sample.int | 226µs | 258µs | 3418.650 | 41.6KB | 2.014526 |
| sample_prob | 392µs | 410µs | 2298.579 | 46.8KB | 2.014530 |
plot(bm)Loading required namespace: tidyr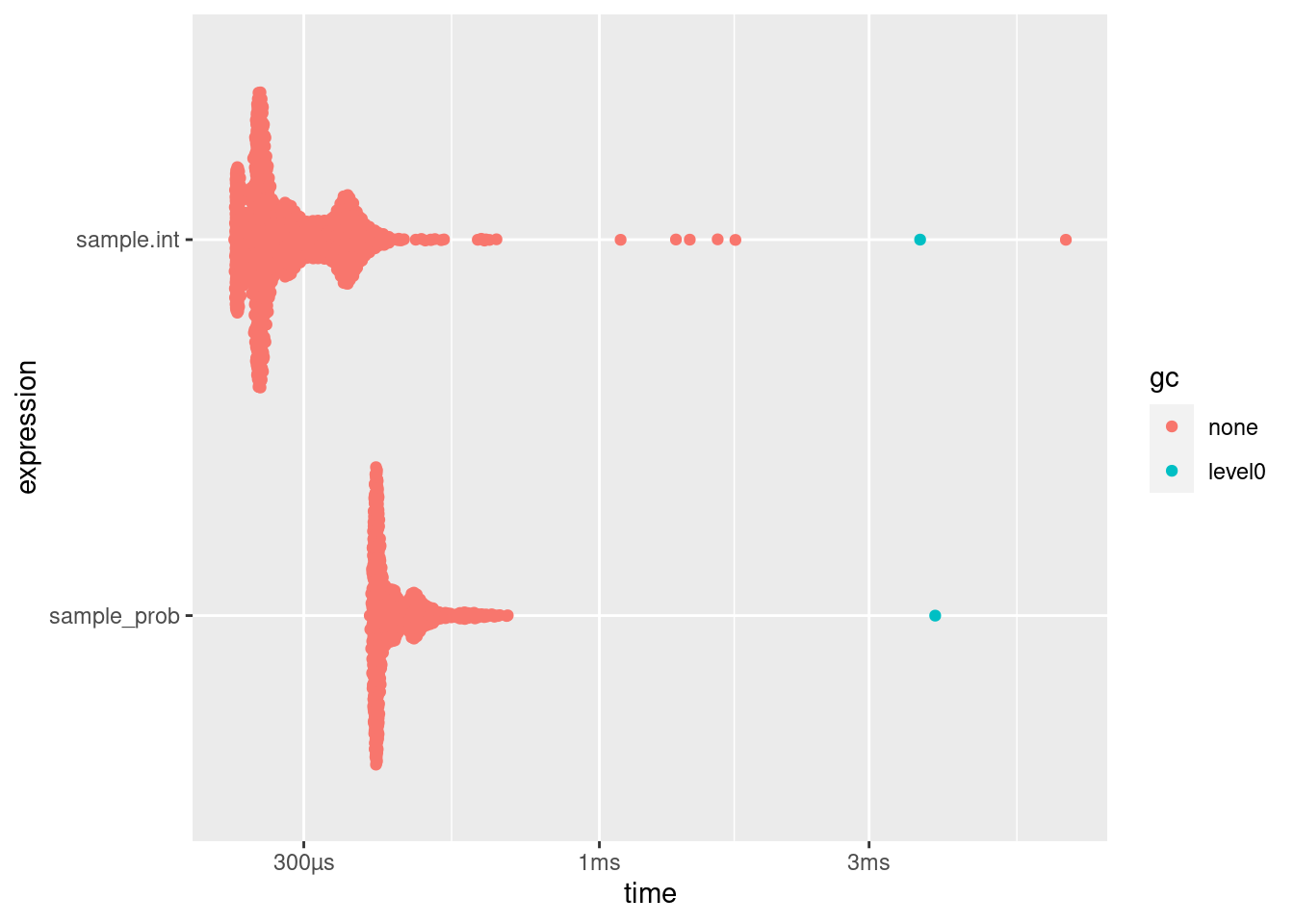
There is only little difference between R’s build in method and this algorithm for only ten different possibilities. However, any performance advantage of stochastic acceptance should come from \(O(1)\) scaling, i.e. larger number of possibilities are more interesting:
N <- 1e5
prob <- runif(N)
bm <- bench::mark(
sample.int = sample.int(N, M, replace = TRUE, prob = prob),
sample_prob = sample_prob(M, prob = prob),
check = FALSE
)
knitr::kable(bm[, 1:6])| expression | min | median | itr/sec | mem_alloc | gc/sec |
|---|---|---|---|---|---|
| sample.int | 2.75ms | 3.6ms | 273.1216 | 1.19MB | 6.302807 |
| sample_prob | 739.42µs | 791.6µs | 1146.1369 | 41.6KB | 0.000000 |
plot(bm)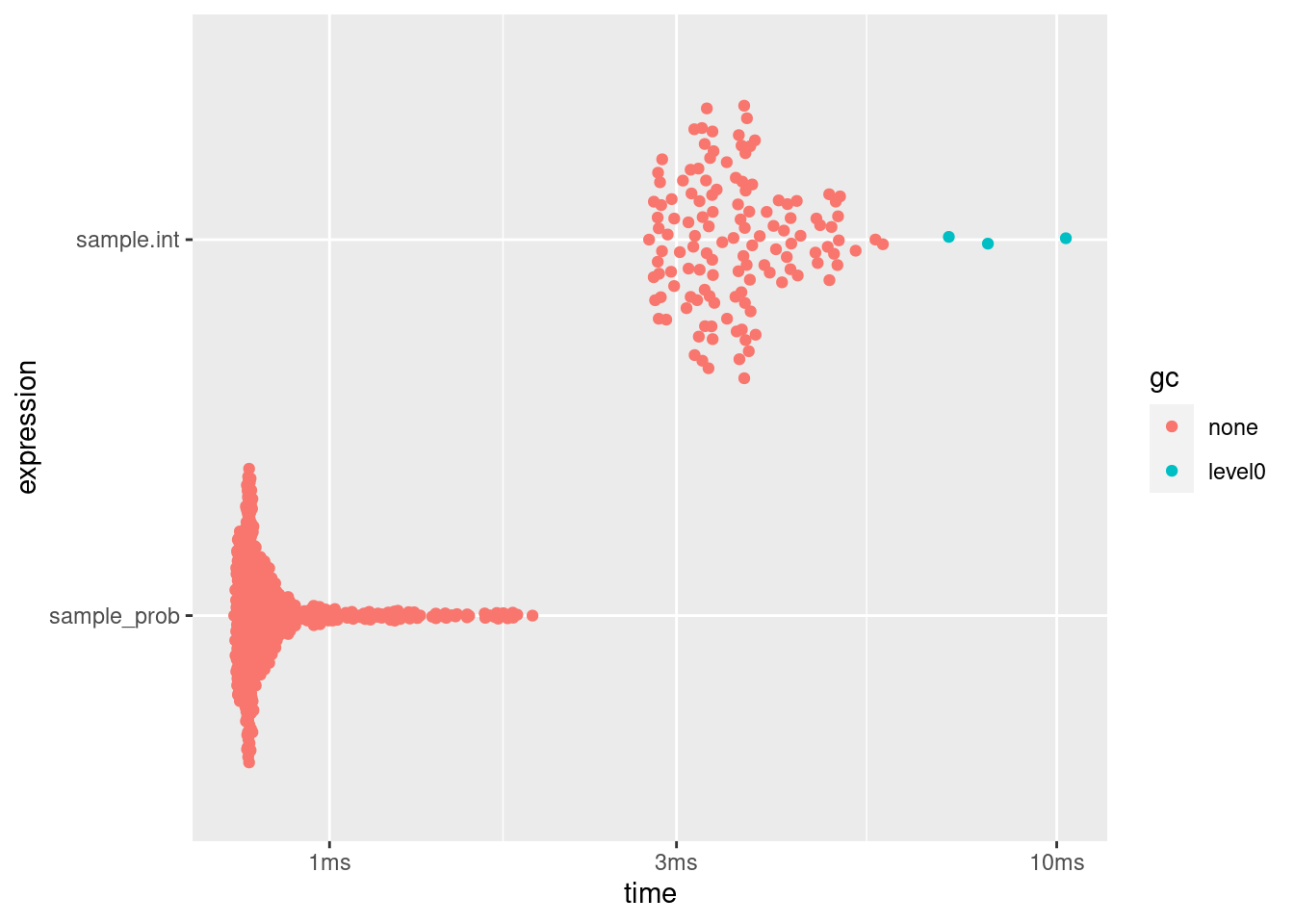
This is very promising! It looks worthwhile including this algorithm into {dqrng}, especially since it can also be used for weighted sampling without replacement.