#include <Rcpp.h>
using namespace Rcpp;
// [[Rcpp::export]]
IntegerVector do_pmax0_abs_int(IntegerVector x) {
R_xlen_t n = x.length();
IntegerVector out(clone(x));
for (R_xlen_t i = 0; i < n; ++i) {
int oi = out[i];
out[i] += abs(oi); // integer overflow possible!
out[i] /= 2;
}
return out;
}The so called XY problem is a classical situation on Q&A sites such as stackoverflow. While answering a recent question there I thought to have spotted such a case and addressed the actual problem. As it turns out, I had stopped too early when going for the root cause.
The question asker wanted to speed up the evaluation of pmax(x, 0) for an integer vector x by using the identity pmax(x, 0) = (x + abs(x)) / 2 and going to C++ with the help of Rcpp:
The issue with this initial solution is the potential for an integer overflow for values larger than half the maximum size of a 32bit integer, i.e. \(2^{30} = 1,073,741,824\), resulting in negative results:
set.seed(42)
ints <- as.integer(runif(1e6, -.Machine$integer.max, .Machine$integer.max))
head(ints)[1] 1781578390 1877224605 -918523703 1419261746 608792367 82016476do_pmax0_abs_int(head(ints))[1] -365905258 -270259043 0 -728221902 608792367 82016476So the original question was how to “quickly determine the approximate maximum of an integer vector”, in particular whether or not the maximum of the integers is not larger than 1,073,741,824.
Reading this question I realized that finding this approximate maximum would require scanning the vector linearly with the potential for an early exit. In the worst case we would compare every vector element with some fixed number, which is exactly what we wanted to avoid in the first place! In addition, it was unclear to me how one could make use of this approximate maximum. On the other hand, it is quite easy to fix the potential integer overflow by using a larger integer type for intermediate results:
#include <Rcpp.h>
using namespace Rcpp;
// [[Rcpp::plugins(cpp11)]]
// [[Rcpp::export]]
IntegerVector do_pmax0_abs_int64(IntegerVector x) {
R_xlen_t n = x.length();
IntegerVector out = no_init(n);
for (R_xlen_t i = 0; i < n; ++i) {
int64_t oi = x[i];
oi += std::abs(oi);
out[i] = static_cast<int>(oi / 2);
}
return out;
}Since this version skips the initialization of the output vector, it is faster than the original solution and works correctly for for large integers:
| expression | min | median | itr/sec | mem_alloc |
|---|---|---|---|---|
| pmax(ints, 0) | 10.16ms | 16.07ms | 65.68012 | 15.34MB |
| do_pmax0_abs_int(ints) | 1.8ms | 3.54ms | 269.19683 | 3.82MB |
| do_pmax0_abs_int64(ints) | 1.23ms | 2.98ms | 344.47693 | 3.82MB |
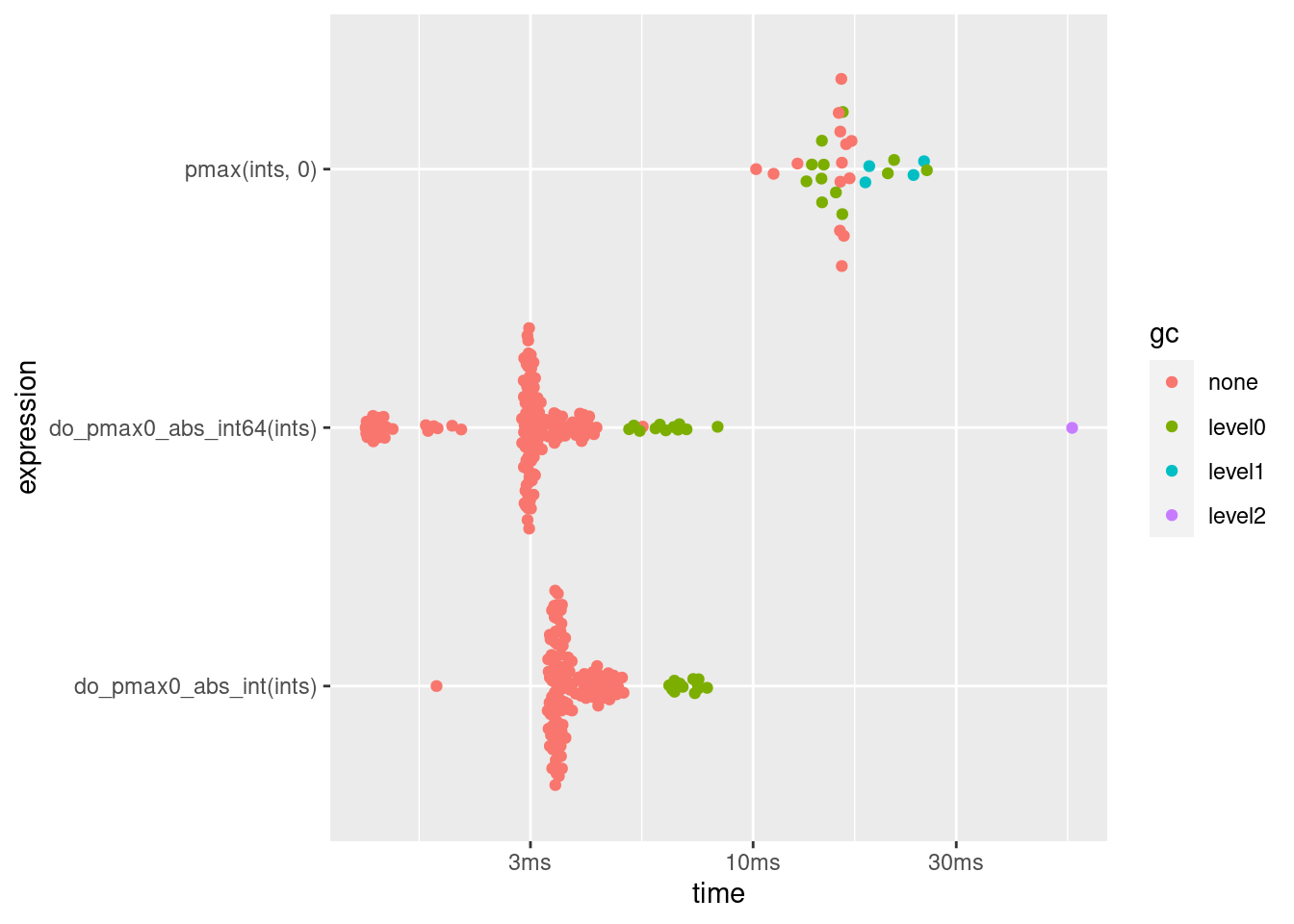
At this point I stopped and posted my answer, even though I should have looked at at least two other things. First, why does pmax uses so much more memory? The reason is a classical error when working with R: 0 is not an integer but a numeric. To compare with the integer one should use 0L. This reduces memory consumption and run time, but the latter is still larger than for the C++ solutions.
Second and more importantly, is the mathematical trick from the beginning really needed? Can one not simply traverse the vector and take the maximum for each element compared to zero?
#include <Rcpp.h>
using namespace Rcpp;
// [[Rcpp::plugins(cpp11)]]
// [[Rcpp::export]]
IntegerVector do_pmax0_int(IntegerVector x) {
IntegerVector out = no_init(x.length());
std::transform(x.cbegin(), x.cend(), out.begin(),
[](int y){return std::max(y, 0);});
return out;
}It turns out that this is actually the fastest method:
| expression | min | median | itr/sec | mem_alloc |
|---|---|---|---|---|
| do_pmax0_int(ints) | 846.55µs | 2.39ms | 480.4942 | 3.82MB |
| do_pmax0_abs_int64(ints) | 1.23ms | 2.92ms | 395.5972 | 3.82MB |
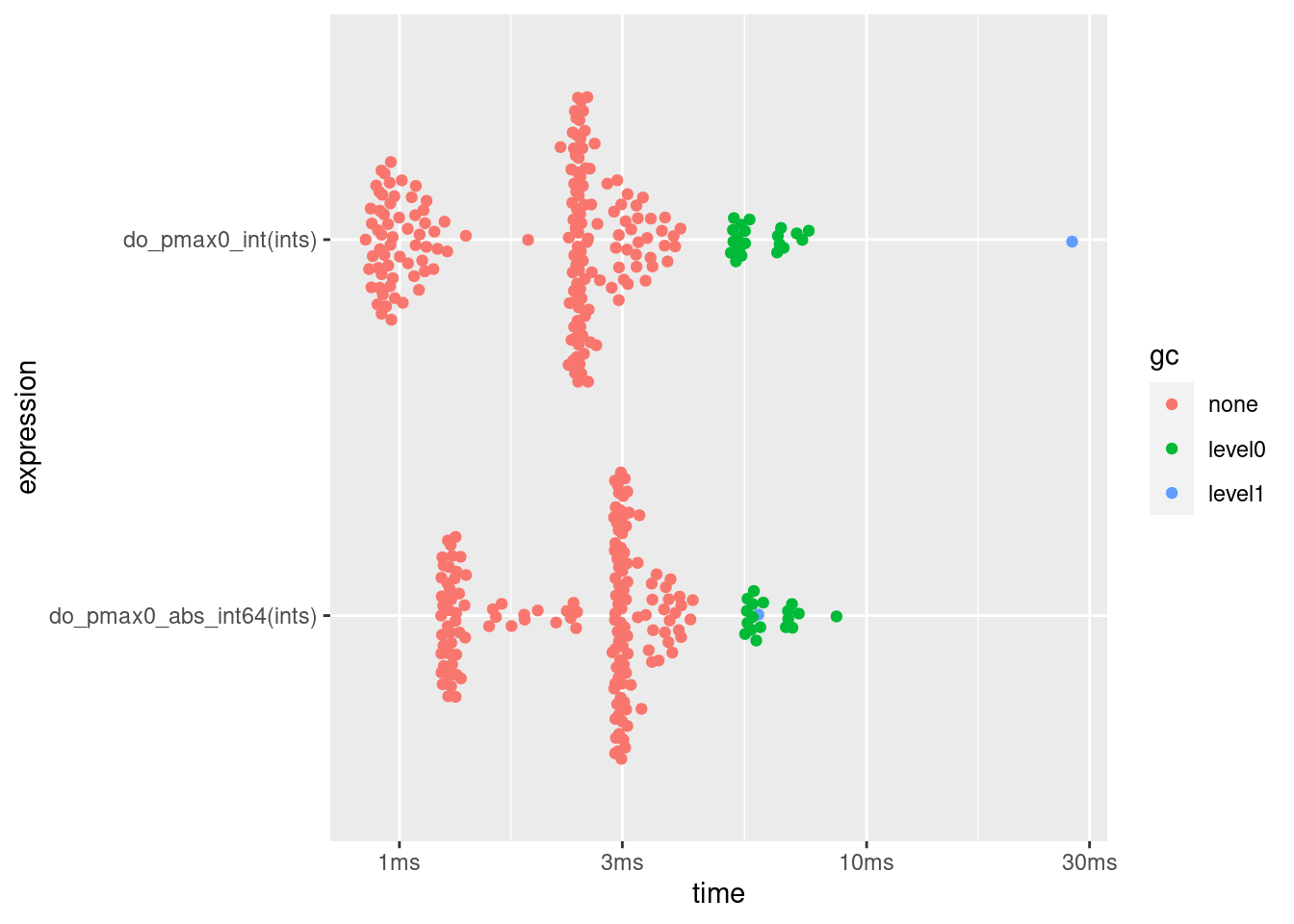
While avoiding the first level XY problem in the question, I initially did not notice the second level XY problem.