Numerical integration over an infinite interval in Rcpp

On Stack Overflow the question was asked how to numerically integrate a function over a infinite range in Rcpp, e.g. by using RcppNumerical. As an example, the integral

\[ \int_{-\infty}^{\infty} \mathrm{d}x \exp\left(-\frac{(x-\mu)^4}{2}\right) \]

was given. Using RcppNumerical is straight forward. One defines a class that extends Numer::Func for the function and an interface function that calls Numer::integrate on it:

// [[Rcpp::depends(RcppEigen)]]
// [[Rcpp::depends(RcppNumerical)]]
#include <RcppNumerical.h>
class exp4: public Numer::Func {
private:
    double mean;
public:
    exp4(double mean_) : mean(mean_) {}
    
    double operator()(const double& x) const {
        return exp(-pow(x-mean, 4) / 2);
    }
};

// [[Rcpp::export]]
Rcpp::NumericVector integrate_exp4(const double &mean, const double &lower, const double &upper) {
    exp4 function(mean);
    double err_est;
    int err_code;
    const double result = Numer::integrate(function, lower, upper, err_est, err_code);
    return Rcpp::NumericVector::create(Rcpp::Named("result") = result,
                                       Rcpp::Named("error") = err_est);
}

This works fine for finite ranges:

integrate_exp4(4, 0, 4)

      result        error 
1.077900e+00 9.252237e-08

However, it produces NA for infinite ones:

integrate_exp4(4, -Inf, Inf)

      result        error 
2.155801e+00 1.439771e-06

This is disappointing, since base R’s integrate() handles this without problems:

exp4 <- function(x, mean) exp(-(x - mean)^4 / 2)
integrate(exp4, 0, 4, mean = 4)

1.0779 with absolute error < 1.3e-07

integrate(exp4, -Inf, Inf, mean = 4)

2.155801 with absolute error < 7.9e-06

In this particular case the problem can be easily solved in two different ways. First, the integral can be expressed in terms of the Gamma function:

\[ \int_{-\infty}^{\infty} \mathrm{d}x \exp\left(-\frac{(x-\mu)^4}{2}\right) = 2^{-\frac{3}{4}} \Gamma\left(\frac{1}{4}\right) \approx 2.155801 \]

Second, the integrand is almost zero almost everywhere:

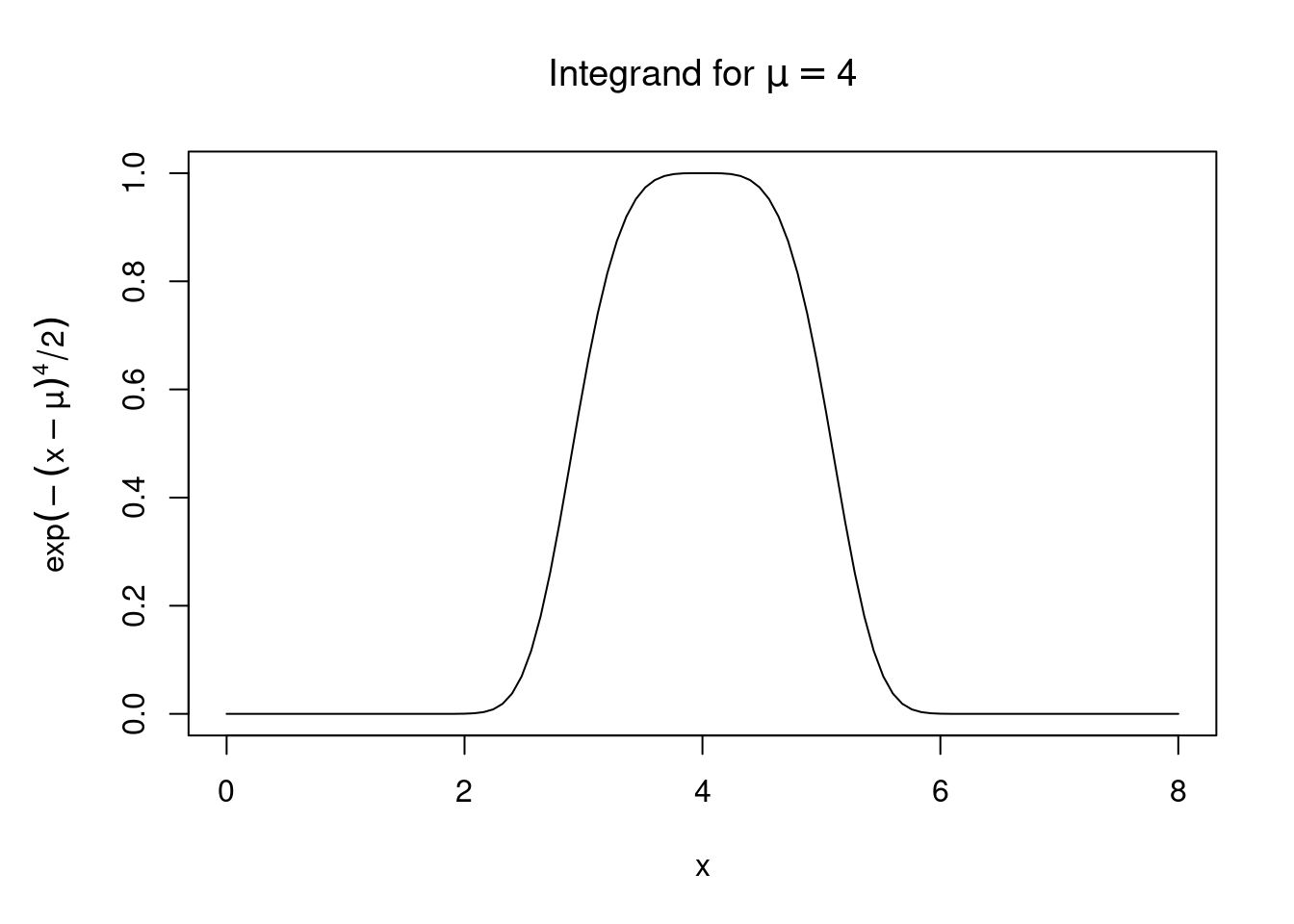
It is therefore sufficient to integrate over a small region around mean to get a reasonable approximation for the integral over the infinite range:

integrate_exp4(4, 1, 7)

      result        error 
2.155801e+00 9.926448e-13

However, the trick to approximate the integral over an infinite range with an integral over a (possibly large) finite range does not work for functions that approach zero more slowly. The help page for integrate() has a nice example for this effect:

## a slowly-convergent integral
integrand <- function(x) {1/((x+1)*sqrt(x))}
integrate(integrand, lower = 0, upper = Inf)

3.141593 with absolute error < 2.7e-05

## don't do this if you really want the integral from 0 to Inf
integrate(integrand, lower = 0, upper = 10)

2.529038 with absolute error < 3e-04

integrate(integrand, lower = 0, upper = 100000)

3.135268 with absolute error < 4.2e-07

integrate(integrand, lower = 0, upper = 1000000, stop.on.error = FALSE)

failed with message 'the integral is probably divergent'

How does integrate() handle the infinite range and can we replicate this in Rcpp? The help page states:

If one or both limits are infinite, the infinite range is mapped onto a finite interval.

This is in fact done by a different function from R’s C-API: Rdqagi() instead of Rdqags(). In principle one could call Rdqagi() via Rcpp, but this is not straightforward. Fortunately, there are at least two other solutions.

The GNU Scientific Library provides a function to integrate over the infinte interval \((-\infty, \infty)\), which can be used via the RcppGSL package:

// [[Rcpp::depends(RcppGSL)]]
#include <RcppGSL.h>
#include <gsl/gsl_integration.h>

double exp4 (double x, void * params) {
    double mean = *(double *) params;
    return exp(-pow(x-mean, 4) / 2);
}

// [[Rcpp::export]]
Rcpp::NumericVector normalize_exp4_gsl(double &mean) {
    gsl_integration_workspace *w = gsl_integration_workspace_alloc (1000);
    
    double result, error;
    
    gsl_function F;
    F.function = &exp4;
    F.params = &mean;
    
    gsl_integration_qagi(&F, 0, 1e-7, 1000, w, &result, &error);
    gsl_integration_workspace_free (w);
    
    return Rcpp::NumericVector::create(Rcpp::Named("result") = result,
                                       Rcpp::Named("error") = error);
}

normalize_exp4_gsl(4)

      result        error 
2.155801e+00 3.718126e-08

Alternatively, one can apply the transformation used by GSL (and probably R) also in conjunction with RcppNumerical. To do so, one has to substitute \(x = (1-t)/t\) resulting in

\[ \int_{-\infty}^{\infty} \mathrm{d}x f(x) = \int_0^1 \mathrm{d}t \frac{f((1-t)/t) + f(-(1-t)/t)}{t^2} \]

Now one could write the code for the transformed function directly, but it is of course nicer to have a general solution, i.e. use a class template that can transform any function in the desired fashion

// [[Rcpp::depends(RcppEigen)]]
// [[Rcpp::depends(RcppNumerical)]]
#include <RcppNumerical.h>
class exp4: public Numer::Func {
private:
    double mean;
public:
    exp4(double mean_) : mean(mean_) {}
    
    double operator()(const double& x) const {
        return exp(-pow(x-mean, 4) / 2);
    }
};

// [[Rcpp::plugins(cpp11)]]
template<class T> class trans_func: public T {
public:
    using T::T;
    
    double operator()(const double& t) const {
        double x = (1-t)/t;
        return (T::operator()(x) + T::operator()(-x))/pow(t, 2);
    }
};

// [[Rcpp::export]]
Rcpp::NumericVector normalize_exp4(const double &mean) {
    trans_func<exp4> f(mean);
    double err_est;
    int err_code;
    const double result = Numer::integrate(f, 0, 1, err_est, err_code);
    return Rcpp::NumericVector::create(Rcpp::Named("result") = result,
                                       Rcpp::Named("error") = err_est);
}

normalize_exp4(4)

      result        error 
2.155801e+00 1.439771e-06

Note that the exp4 class is identical to the one from the initial example. This means one can use the same class to calculate integrals over a finite range and after transformation over an infinite range.